高維少樣本數據降維實用指南

一、引言

在數據分析和機器學習中，高維數據往往包含大量特征，而少樣本數據則意味著數據點較少。高維少樣本數據不僅增加了計算復雜度，還可能引發過擬合等問題。因此，降維成為處理這類數據的關鍵步驟。本文將探討幾種有效的降維方法，并提供詳細的操作步驟。

二、常用降維方法

2.1 主成分分析（PCA）

2.1.1 方法簡介

PCA是一種線性降維技術，通過正交變換將高維數據轉換到新的低維坐標系中，使得新坐標系的第一主成分具有最大的方差，后續主成分方差依次遞減，從而實現降維。

2.1.2 操作步驟

1. 數據標準化：對原始數據進行標準化處理，使每個特征的均值為0，方差為1。
2. 計算協方差矩陣：根據標準化后的數據計算協方差矩陣。
3. 特征值分解：對協方差矩陣進行特征值分解，得到特征值和特征向量。
4. 選擇主成分：根據特征值的大小選擇前k個主成分，即選擇前k個最大的特征值對應的特征向量。
5. 數據轉換：將原始數據投影到選定的k個主成分上，得到降維后的數據。

   2.1.3 注意事項

• PCA是一種無監督降維方法，不考慮數據的標簽信息。
• 選擇主成分時，可根據累計貢獻率（即前k個主成分方差之和占總方差的比例）來確定k值。

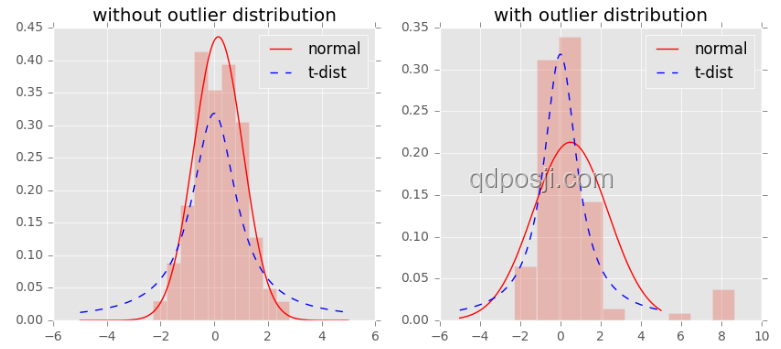
  2.2 t-分布隨機鄰域嵌入（t-SNE）

  2.2.1 方法簡介

  t-SNE是一種非線性降維技術，適用于高維數據的可視化。它通過計算數據點之間的相似度，并將高維數據映射到低維空間中，同時盡量保持數據點之間的相似關系。

  2.2.2 操作步驟

1. 計算相似度：使用高斯核函數計算高維數據點之間的相似度。
2. 構建聯合概率分布：將相似度轉換為聯合概率分布，表示高維空間中數據點之間的相似性。
3. 優化低維表示：在低維空間中構建學生t分布，通過最小化KL散度來優化低維表示，使得低維空間中數據點的相似度與高維空間中的聯合概率分布盡量一致。
4. 設置參數：t-SNE的參數（如困惑度、迭代次數等）對結果有較大影響，需根據具體數據進行調整。

   2.2.3 注意事項

• t-SNE對數據的局部結構敏感，適用于發現數據中的簇或流形結構。
• t-SNE的計算復雜度較高，對于大規模數據可能需要較長時間。

  三、實用技巧和竅門

  3.1 特征選擇

  在進行降維之前，可以先進行特征選擇，去除冗余或不重要的特征。特征選擇方法包括過濾式、包裹式和嵌入式等。過濾式方法基于統計測試或相關性分析來選擇特征；包裹式方法通過構建預測模型來評估特征的重要性；嵌入式方法則在模型訓練過程中自動選擇特征。

  3.2 降維方法組合

  對于復雜的高維少樣本數據，可以嘗試將多種降維方法組合使用。例如，可以先使用PCA進行初步降維，再使用t-SNE進行可視化。組合使用可以充分利用各種方法的優點，提高降維效果。

  

  3.3 參數調優

  降維方法的參數對結果有很大影響。例如，PCA中的主成分個數、t-SNE中的困惑度和迭代次數等。可以通過交叉驗證等方法來調優參數，找到最佳的降維方案。

  四、實際案例

  4.1 案例背景

  假設我們有一個包含100個樣本、每個樣本有50個特征的高維數據集。由于樣本數量較少，直接使用高維數據進行模型訓練可能會導致過擬合。因此，我們需要對數據進行降維處理。

  4.2 PCA降維案例

1. 數據標準化：使用sklearn.preprocessing.StandardScaler對數據進行標準化處理。
2. PCA降維：使用sklearn.decomposition.PCA進行PCA降維，選擇前10個主成分。

   from sklearn.preprocessing import StandardScaler
   from sklearn.decomposition import PCA
   import numpy as np
   # 假設X為高維數據集
   scaler = StandardScaler()
   X_scaled = scaler.fit_transform(X)
   pca = PCA(n_components=10)
   X_pca = pca.fit_transform(X_scaled)
   print("降維后的數據形狀：", X_pca.shape)

3. 結果分析：降維后的數據形狀為(100, 10)，即100個樣本、每個樣本有10個特征。

   4.3 t-SNE可視化案例

4. 數據預處理：使用PCA將數據降到較低維度（如20維），以減少t-SNE的計算復雜度。
5. t-SNE可視化：使用sklearn.manifold.TSNE進行t-SNE可視化。

   from sklearn.manifold import TSNE
   import matplotlib.pyplot as plt
   # 假設X_pca為PCA降維后的數據
   tsne = TSNE(n_components=2, perplexity=30, n_iter=300)
   X_tsne = tsne.fit_transform(X_pca)
   plt.scatter(X_tsne[:, 0], X_tsne[:, 1])
   plt.title("t-SNE可視化")
   plt.xlabel("Component 1")
   plt.ylabel("Component 2")
   plt.show()

6. 結果分析：通過t-SNE可視化，我們可以直觀地看到數據在低維空間中的分布，有助于發現數據中的簇或流形結構。

   五、注意事項和常見問題解答（FAQ）

   5.1 注意事項

• 在選擇降維方法時，應根據數據的特性和需求進行選擇。例如，對于線性可分的數據，PCA可能效果更好；對于非線性結構的數據，t-SNE可能更合適。
• 降維后的數據可能丟失一些原始信息，因此需要在降維效果和信息保留之間找到平衡。
• 在使用t-SNE等復雜降維方法時，應注意計算資源和時間的消耗。

  5.2 常見問題解答

  Q1：PCA降維后數據維度如何選擇？ A1：可以根據累計貢獻率來確定PCA降維后的數據維度。一般來說，累計貢獻率達到90%以上時，可以認為降維后的數據保留了大部分原始信息。 Q2：t-SNE中的困惑度參數如何設置？ A2：困惑度參數控制t-SNE在高維空間中數據點之間的相似度分布。困惑度越大，t-SNE越關注數據點的全局結構；困惑度越小，t-SNE越關注數據點的局部結構。一般來說，困惑度可以設置為數據點數量的平方根附近的一個值，并通過實驗進行調整。 Q3：降維后數據能否用于模型訓練？ A3：降維后的數據可以用于模型訓練，但需要注意降維過程中可能丟失的信息對模型性能的影響。在訓練模型時，可以結合交叉驗證等方法來評估降維效果。 圖1：PCA降維示意圖 通過本文的介紹，相信您已經對高維少樣本數據的降維方法有了更深入的了解。在實際應用中，可以根據數據特性和需求選擇合適的降維方法，并通過參數調優和特征選擇等手段來提高降維效果。希望本文能對您有所幫助！